扩散模型是如何工作的：从零开始的数学原理

译者前言

基于生成对抗网络 GANs 的 AI 生成图像往年在互联网不温不热，但就在最近这几个月， Open AI 于 2022 年 4 月初发布的 DALL-E 2 (基于 GPT Model) ，以及 stability.ai在新窗口打开于 2022 年 8 月底发布的 Stable Diffusion (基于 Diffusion Models) ，其生成的照片、画作的效果让人乍舌，随即引发了一股新的互联网 AI 创作热潮。

引发这一系列热潮的便是 Novel AI在新窗口打开于 2022 年 10 月初发布的，能够画各种精致二次元风格图片的 NovelAI Diffusion (基于 Stable Diffusion) 一下子把 AI 绘画推向风口浪尖。无数乐子人蜂拥而至，甚至有黑客把 Novel AI 的官网源码和模型全部扒了下来。 AI 创作数量极快，乍一看都很精致，而这些 “AI Based” 作品正在以一种极快的速度挤压创作者的空间，随即引发的便是关于伦理道德和法律的一系列疑问。

但是本文暂不讨论伦理道德等方面的问题（也许之后会写一篇文章讨论），仅仅先从技术角度和数学原理上简要介绍效果出众、“秒杀” GANs 且改变了人们对原本 AI 绘画认知的 Diffusion Models 的数学原理。

扩散模型是什么？

扩散模型 (Diffusion Models) 是一种新型的、先进的生成模型，可以生成各种高分辨率图像。在 OpenAI, Nvidia 和 Google 成功地训练了大规模的模型后，扩散模型已经吸引了很多人的注意。基于扩散模型的架构有 GLIDE, DALLE-2, Imagen 和完全开源的 Stable Diffusion 。

其背后的原理是什么？

在这篇文章，我们将从基本原理开始挖掘。目前已经有许多不同的基于扩散模型的架构，我们将重点讨论其中最突出的一个，即由 Sohl-Dickstein et al在新窗口打开和 Ho. et al 2020在新窗口打开提出的去噪扩散概率模型 (DDPM, denoising diffusion probabilistic model) 。其它各种方法将不会具体讨论，如 Stable Diffusion 和 score-based models 。

提示

扩散模型与之前所有的生成方法有着本质的区别。直观地说，它们旨在将图像生成过程（采样）分解为许多小的“去噪”步骤

直观点说，模型可以在这些小的步骤中自我修正，并逐渐产生一个更好的样本。在某种程度上，这种完善表征的想法已经在 alphafold在新窗口打开等模型中得到了应用。但是，这种迭代过程使其采样速度很慢，至少与 GANs在新窗口打开相比。

扩散过程

扩散模型的基本思想是相当简单的。把输入图像并通过一系列的步骤，逐渐向其添加高斯噪声，我们将此称为正向过程。值得注意的是，正向过程与神经网络的正向传播无关，但是正向传播对于为我们的神经网络生成目标（应用噪声步骤后的图像）是有必要的。

之后，神经网络被训练为通过逆转噪声过程来恢复原始数据。通过对反向过程进行建模，我们可以生成新的数据。这就是所谓的反向扩散过程，或者说是生成式模型的采样过程。

具体是怎样的？让我们深入其中的数学，让一切变得清晰起来。

前向扩散

扩散模型可以被看作是潜在变量模型。“潜在”意味着我们指的是一个隐藏的连续特征空间。以这种方式，扩散模型可能看起来类似于变分自动编码器 (VAEs)在新窗口打开。

在实践中，前向扩散是用一个马尔科夫链的步骤来制定的。这里，马尔可夫链意味着每一步只取决于前一步，这是一个很自然的假设。重要的是，与基于流量的模型不同，我们不受限制地使用特定类型的神经网络。

给定一个数据点，从真实数据分布 () 中采样，我们可以通过添加噪声来定义一个前向扩散过程。具体来说，在马尔科夫链的每一步，我们向添加方差为的高斯噪声，产生一个新的潜在变量，其分布为。这个扩散过程可以表述如下：

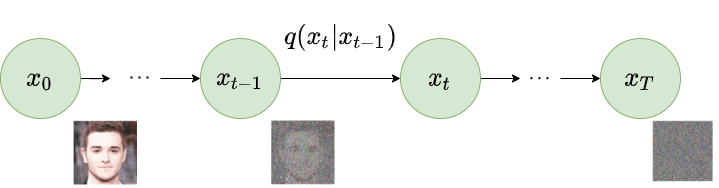
前向扩散过程
图片修改自 Ho et al. 2020在新窗口打开

由于我们处于多维情况下，是单位矩阵，表明每个维度有相同的标准偏差。注意到，是一个正态分布，其均值是，方差为，其中是一个对角矩阵的方差（这里就是）。

因此，我们可以自到以一种可操作的方式来近似输入。在数学上，这种后验概率定义如下：

其中，意味着我们从时间到重复应用。

到目前为止，看起来还不错？并不！对于时间步长我们需要为了采样应用函数 500 次。难道就没有更好的方式吗？

重参数化技巧 (Reparametrization Trick)在新窗口打开对此提供了一个魔法般的补救办法。

重参数化技巧：在任何时间步长上的可操作闭式采样

如果我们定义 , ，其中，那么我们可以使用重参数化技巧证明：

注

由于所有时间段都有相同的高斯噪声，我们从现在开始只使用符号

因此，为了产生一个样本，我们可以使用如下公式：

由于是一个超参数，我们可以预先计算所有时间步长的和。这意味着我们在任何一个时间点对噪声进行采样，并一次性得到。因此，我们可以在任何一个任意的时间段对我们的潜变量进行采样。这将是我们以后计算可操作的目标损失的目标。

方差表

方差参数可以固定为一个常数，也可以选择作为时间段的一个时间表。事实上，人们可以定义一个方差表，它可以是线性的、二次的、余弦的等等。最初的 DDPM 作者利用了一个从到增加的线性时间表。 Nichol et al. 2021在新窗口打开的研究表明，采用余弦时间表效果更好。

分别来自线性（上面）和余弦时间表（下面）的潜伏样本
图片来自 Nichol & Dhariwal 2021在新窗口打开

反向扩散

当时，潜在的几乎是一个各向同性 (isotropic)在新窗口打开的高斯分布。因此，如果我们设法学习反向分布，我们可以对进行采样，从中获取样本，运行反向过程并从，从原始数据分布中产生一个新的数据点。

问题是我们如何对反向扩散过程进行建模。

用神经网络逼近反向过程

在实际情况中，我们不知道，由于估计需要涉及数据分布的计算，所以这是难以解决的。

相反，我们用一个参数化的模型（例如一个神经网络）来近似。由于也将是高斯的，对于足够小的，我们可以选择是高斯的，只需对平均值和方差进行参数化：

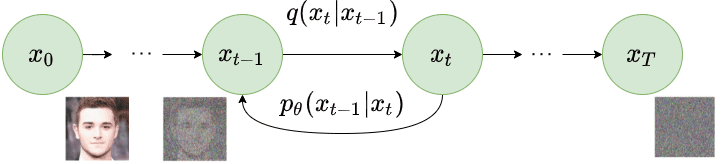
反向扩散过程
图片修改自 Ho et al. 2020在新窗口打开

如果我们对所有的时间步数应用反向公式，我们可以由得到数据分布：

通过对时间段的额外调节，该模型将学会预测每个时间段的高斯参数（指平均值）和协方差矩阵但我们如何训练这样一个模型呢？

训练一个扩散模型

如果我们退一步讲，我们可以注意到，和的组合与变分自编码器 (VAE) 非常相似。因此，我们可以通过优化训练数据的负对数似然来训练它。经过一系列的计算（我们在此不做分析），我们可以把证据下界 (ELBO) 写成如下：

我们来分析一下这些内容：

可以当作是一个重建项 (reconstruction term) ，类似于变量自动编码器 ELBO 中的那个。在 Ho et al 2020在新窗口打开的研究中，这一项是用一个单独的解码器学习的。
显示了与标准高斯是多么的相似。注意到，整个项都没有可训练的参数，因此，训练过程这个项会被忽略。
最后的第三项也表示为，描述了期望的去噪步骤与近似项之间的差异。

很明显，通过 ELBO ，最大化的可能性可以归结为学习去噪步骤。

注

尽管是难以解决的，但 Sohl-Dickstein et al在新窗口打开说明，通过对的附加条件，可以使它变得容易解决

直观地说，画家（这个模型）需要一个参考图像 () 来慢慢绘制（反向扩散步骤）一个图像。因此，当且仅当我们有作为参考时，我们可以向后退一小步，即从噪声中生成一个图像。

换句话说，我们可以在噪声水平的条件下对进行采样。由于和，我们可以证明：

注

和只取决于，所以它可以被预先计算出来

这个小技巧为我们提供了一个完全可操作的 ELBO 。上述属性还有一个重要的副作用，正如我们在重参数化技巧中已经看到的，我们可以将表示为：

其中

通过合并最后两个方程，现在每个时间步长将有一个平均数（我们的目标），它只取决于 :

因此，我们可以使用一个神经网路来近似并得到如下均值结果：

因此，损失函数（ELBO中的去噪项）可以表示为：

这实际上告诉我们，该模型不是预测分布的平均值，而是预测每个时间点的噪声

Ho et.al 2020在新窗口打开对实际损失项做了一些简化，因为他们忽略了一个加权项。简化后的版本优于完整的目标：

作者发现，优化上述目标比优化原始 ELBO 效果更好。这两个方程的证明可以在 Lillian Weng在新窗口打开的这篇优秀文章或 Luo et al. 2022在新窗口打开中找到。

此外，Ho et. al 2020在新窗口打开决定保持方差固定，让网络只学习均值。后来 Nichol et al. 2021在新窗口打开对此进行了改进，他们让网络学习协方差矩阵（通过修改），取得了更好的结果。

DDPMs 的训练和采样算法
图片来自 Ho et al. 2020在新窗口打开

架构

到目前为止，我们还没有提到的一件事是模型的架构是什么样子的。请注意，模型的输入和输出应该是相同大小的。

为此， Ho et al.在新窗口打开采用了一个 U-Net 。如果你对 U-Net 不熟悉，请随时查看我们过去关于主要 U-Net 架构在新窗口打开的文章。简而言之， U-Net 是一种对称的架构，其输入和输出的空间大小相同，在相应特征维度的编码器和解码器块之间使用跳过连接在新窗口打开。通常情况下，输入图像首先被降频，然后被升频，直到达到其初始尺寸。

在 DDPMs 的原始实现中， U-Net 由宽 ResNet 块在新窗口打开、分组归一化在新窗口打开以及自我注意在新窗口打开块组成。

扩散时间段是通过在每个残差块中加入一个正弦的位置嵌入在新窗口打开来指定的。欲了解更多细节，请随时访问官方 GitHub 仓库在新窗口打开。关于扩散模型的详细实现，请查看 Hugging Face 的这篇精彩文章在新窗口打开。

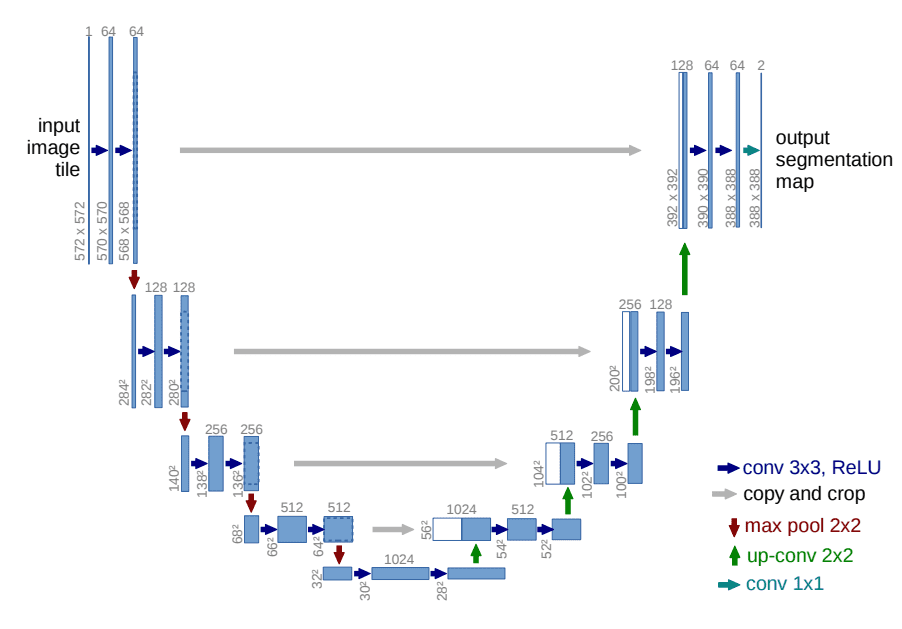
U-Net 的架构
图片来自 Ronneberger et al.在新窗口打开

条件性图像生成：引导扩散

图像生成的一个关键方面是调节采样过程，以操纵生成的样本。在这里，这也被称为引导性扩散。

甚至有一些方法将图像嵌入到扩散中，以便“引导”生成。从数学上讲，引导指的是用一个条件，即类别标签或图像/文本嵌入来调节先验数据分布，导致为了把扩散模型变成一个条件扩散模型，我们可以在每个扩散步骤中加入条件信息 :

在每个时间点都能看到调节的事实，这可能是文字提示的优秀样本的一个很好的理由。

一般来说，引导扩散模型的目的是学习，所以使用贝叶斯规则，我们可以写出：

因为梯度算子只代表，被移除，所以没有梯度。此外请记住。

再加上一个指导性的标量项，我们就有：

利用这一表述，让我们对分类器和无分类器的引导进行区分。接下来，我们将介绍两个旨在注入标签信息的方法系列。

分类指导

Sohl-Dickstein et al.在新窗口打开以及后来的 Dhariwal 和 Nichol在新窗口打开表明，我们可以使用第二个模型，即分类器，在训练过程中引导向目标类的扩散。为了达到这个目的，我们可以在噪声图像上训练一个分类器，以预测其类别。然后我们可以使用梯度来引导扩散。具体怎么办呢？

我们可以建立一个具有均值和方差的类条件扩散模型。

由于，我们可以用上一节的引导公式表明，均值受到了类的的梯度扰动，而结果是：

在 Nichol et al. 著名的 GLIDE 论文在新窗口打开中，作者扩展了这个想法，并使用 CLIP 嵌入在新窗口打开来指导扩散。 Saharia et al.在新窗口打开提出的 CLIP 由一个图像编码器和一个文本编码器组成。它分别产生一个图像和文本嵌入和，其中是文本标题。

因此，我们可以用它们的点积来扰动梯度：

结果是，它们设法将生成过程“引向”用户定义的文本标题。

分类器引导的扩散采样算法
图片来自 Dhariwal & Nichol 2021在新窗口打开

无分类指导

使用与之前相同的表述，我们可以将无分类器的引导扩散模型定义为：

正如 Ho & Salimans在新窗口打开所提议的那样，不需要第二个分类器模型就可以实现指导作用。事实上，他们使用的是完全相同的神经网络，而不是训练一个单独的分类器，作者将条件性扩散模型与无条件性模型一起训练。在训练过程中，他们随机地将类设置为，这样模型就同时接触到了有条件和无条件的设置：

注

请注意，这也可以用来“注入”文本嵌入，正如我们在分类器指导中显示的那样

这个公认的“怪异”过程有两个主要优点：

它只使用一个单一的模型来指导扩散。
当对难以用分类器预测的信息（如文本嵌入）进行调节时，它简化了指导。

Saharia et al.在新窗口打开提出的 Imagen 在很大程度上依赖于无分类器的引导，因为他们发现这是一个关键因素去产生具有强大图像-文本对准的生成样本。关于 Imagen 方法的更多信息，请看 AI Coffee Break 与 Letitia 的这段 YouTube 视频：

提示

如果长时间加载不出来，说明你的网络无法访问 YouTube

YouTube 视频

扩大扩散模型的规模

你可能会问这些模型的问题是什么。好吧，将这些 U-Net 扩展到高分辨率的图像中，在计算上是非常昂贵的。这给我们带来了两种将扩散模型扩展到高分辨率的方法：级联扩散模型和潜伏扩散模型。

级联扩散模型

Ho et al. 2021在新窗口打开引入了级联扩散模型，以努力产生高保真的图像。级联扩散模型包括一个由许多连续扩散模型组成的管道，生成分辨率越来越高的图像。每个模型通过连续地对图像进行上采样并增加更高分辨率的细节，生成一个比前一个质量更好的样本。为了生成一个图像，我们从每个扩散模型中依次取样。

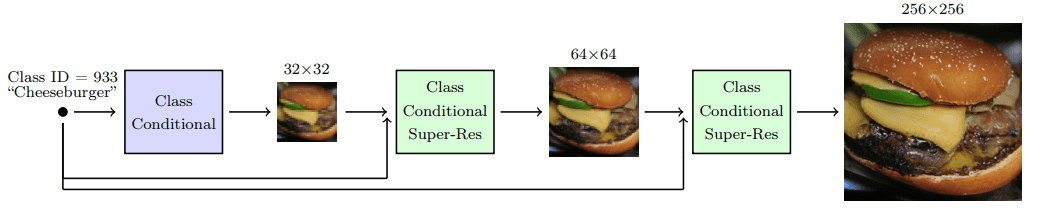
级联扩散模型管道
图片来自 Ho & Saharia et al.

为了获得级联架构的良好效果，对每个超级分辨率模型的输入进行强有力的数据增强是至关重要的。为什么呢？因为它可以减轻之前级联模型的复合误差，以及由于训练-测试不匹配造成的误差。

研究发现，高斯模糊是实现高保真度的一个关键转变，他们把这种技术称为调节增强。

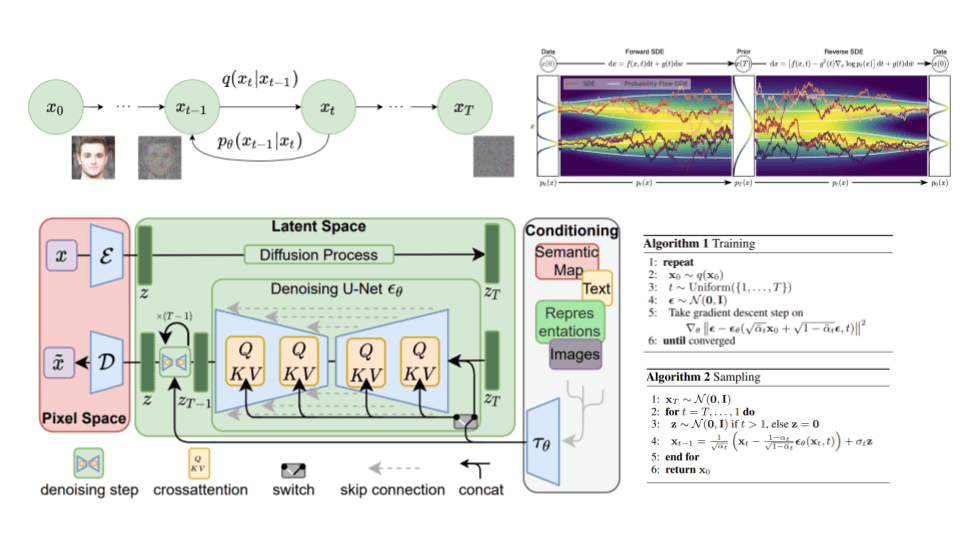
Stable Diffusion: 潜在扩散模型

潜在扩散模型是基于一个相当简单的想法：我们不是直接在高维输入上应用扩散过程，而是将输入投射到一个较小的潜伏空间，并在那里应用扩散。

更详细地说， Rombach et al.在新窗口打开建议使用编码器网络将输入编码为潜伏表示，即。这一决定背后的直觉是通过在低维空间处理输入来降低训练扩散模型的计算需求。之后，一个标准的扩散模型 (U-Net) 应用于生成新的数据，这些数据被一个解码器网络放大。

如果一个典型的扩散模型 (DM) 的损失被表述为：

然后，给定编码器和一个潜在表示，那么一个潜在扩散模型 (LDM) 的损失函数可以表示为：

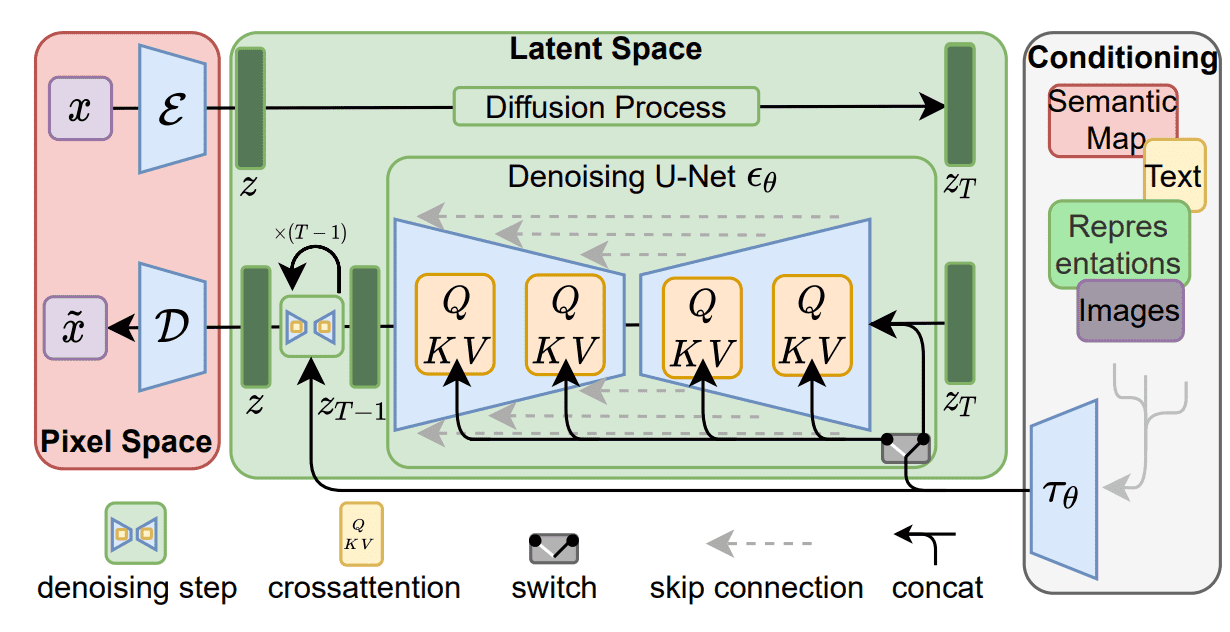
潜伏的扩散模型
图片来自 Rombach et al在新窗口打开

欲了解更多信息，请看这个 YouTube 视频：

提示

如果长时间加载不出来，说明你的网络无法访问 YouTube

YouTube 视频

基于评分的生成模型

在 DDPM 论文发表的同时， Song and Ermon在新窗口打开提出了一种不同类型的生成模型，似乎与扩散模型有许多相似之处。基于评分的模型利用评分匹配和 Langevin 动力学来解决生成式学习。

为基于评分的模型添加噪音：噪声条件得分网络 (NCSN)

提示

到目前为止的问题是：在低密度地区，估计的评分函数通常是不准确的，因为那里的数据点很少。因此，使用 Langevin 动力学采样的数据质量并不好

他们的解决方案是对数据点进行噪声扰动，然后在噪声数据点上训练基于评分的模型。事实上，他们使用了多种规模的高斯噪声扰动。

因此，添加噪声是使 DDPM 和基于评分的模型都能工作的关键。

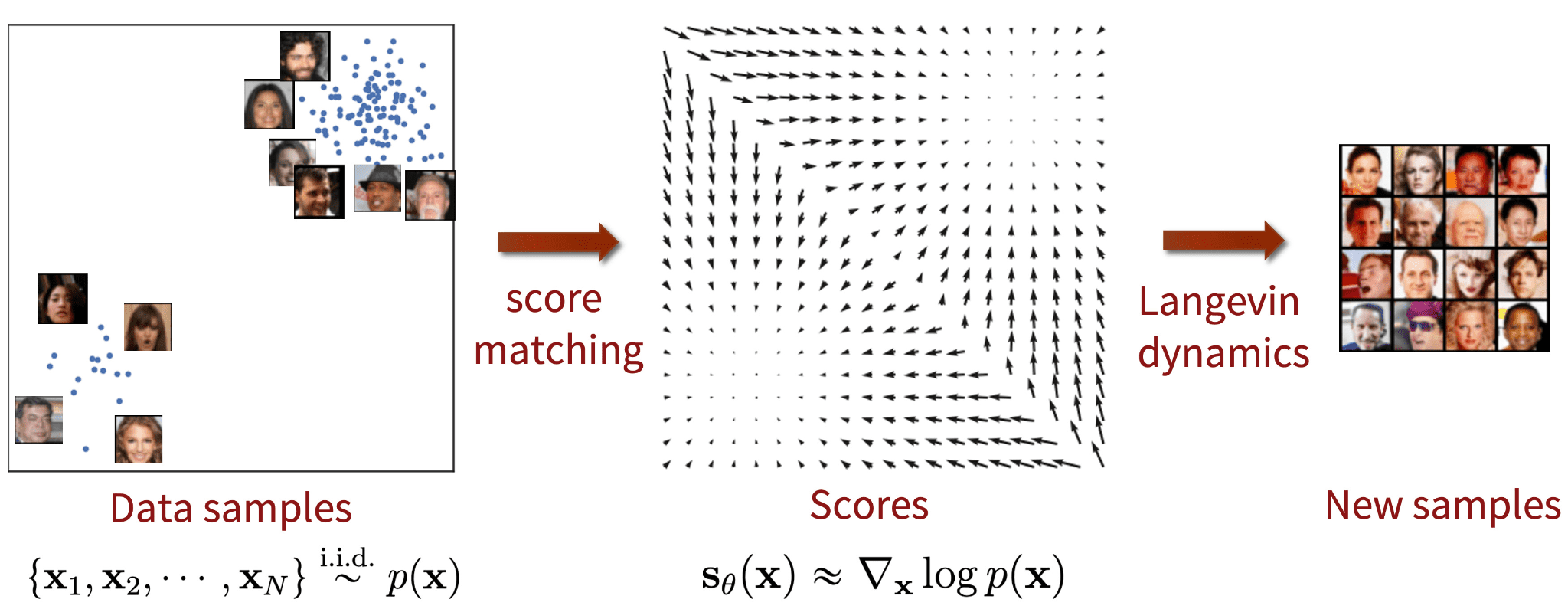
基于评分的生成模型与评分匹配以及 Langevin 动力学
图片来自 Generative Modeling by Estimating Gradients of the Data Distribution在新窗口打开

在数学上，给定数据分布，我们用高斯噪声进行扰动其中得到一个噪声扰动的分布：

然后我们训练一个网络，称为基于噪声条件的评分网络 (NCSN) 来估计评分函数。训练目标是所有噪声尺度的 Fisher 散度在新窗口打开的加权和：

通过随机微分方程 (SDE) 进行基于评分的生成性建模

Song et al. 2021在新窗口打开探讨了基于评分的模型与扩散模型的联系。为了将 NSCNs 和 DDPMs 都囊括在同一伞下，他们提出了以下建议。

我们不使用有限数量的噪声分布来扰动数据，而是使用连续的分布，这些分布根据扩散过程随时间演变。这个过程由一个规定的随机微分方程 (SDE) 来模拟，它不依赖于数据，也没有可训练的参数。通过逆转这个过程，我们可以生成新的样本。

通过随机微分方程 (SDE) 进行基于评分的生成性建模
图片来自 Song et al. 2021在新窗口打开

我们可以把扩散过程定义为以下形式的 SDE:

其中，是维纳过程（又称布朗运动）。是一个矢量值函数，称为的漂移系数，是一个标度函数，称为的扩散系数。请注意， SDE 通常有一个唯一的强解。

提示

为了理解我们为什么使用 SDE ，这里有一个提示： SDE 的灵感来自于布朗运动，在布朗运动中，一些粒子在介质内随机移动。粒子运动的这种随机性模拟了数据上的连续噪声扰动

在对原始数据分布进行足够长时间的扰动后，被扰动的分布会变得接近于一个可操作的噪声分布。

为了产生新的样本，我们需要逆转扩散过程。该 SDE 被选择为有一个相应的封闭形式的反向 SDE:

为了计算反向 SDE ，我们需要估计评分函数。这是用基于评分的模型和 Langevin 动力学完成的。训练目标是 Fisher 分歧的连续组合：

其中表示时间间隔上的均匀分布，是一个正的加权函数。一旦我们有了评分函数，我们就可以把它放入反向 SDE 并求解，以便从原始数据分布中采样。

提示

有许多解决反向 SDE 的方案，我们在此不作分析。请务必查看原始论文或作者的这篇优秀博文在新窗口打开

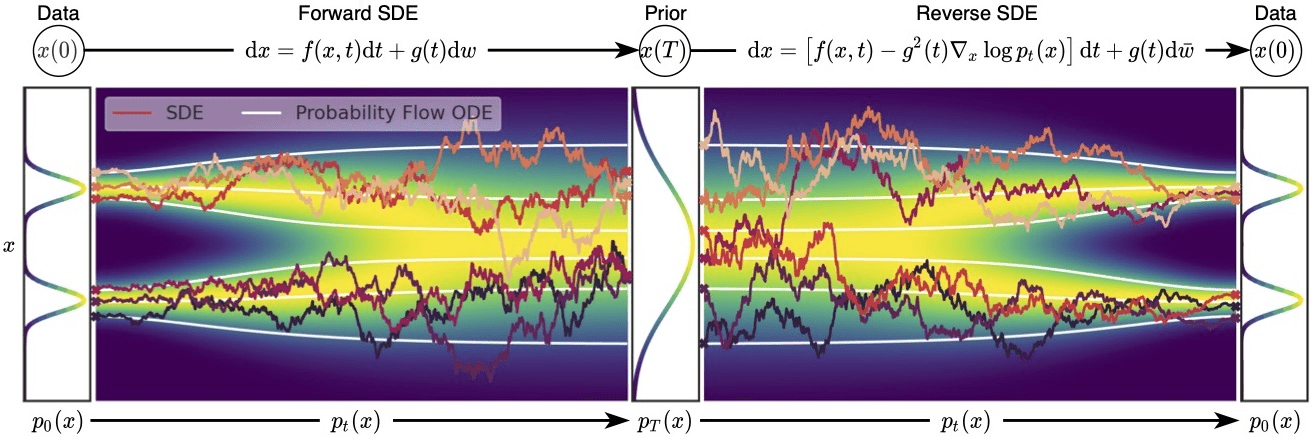
通过 SDEs 进行基于评分的生成性建模的概述
图片来自 Song et al. 2021在新窗口打开

总结

让我们对这篇博文中所学到的主要内容做一个简单的总结。

扩散模型的工作原理是通过一系列的 TT 步骤将高斯噪声逐渐添加到原始图像中，这个过程被称为扩散。
为了对新数据进行采样，我们使用神经网络对反向扩散过程进行近似。
模型的训练是基于证据下界 (ELBO) 的最大化。
我们可以将扩散模型置于图像标签或文本嵌入的条件下，以便“指导”扩散过程。
级联扩散和潜伏扩散是两种将模型扩展到高分辨率的方法。
级联扩散模型是连续的扩散模型，可以生成分辨率越来越高的图像。
潜伏扩散模型（像 Stable Diffusion ）在较小的潜伏空间上应用扩散过程，以提高计算效率，使用变分自编码器进行向上和向下取样。
基于评分的模型也将一连串的噪声扰动应用到原始图像上。但它是用评分匹配和 Langevin 动力学来训练的。尽管如此，它最终的目标是相似的。
扩散过程可以被表述为一个 SDE 。解决反向 SDE 使我们能够生成新的样本。

最后，对于扩散模型在新窗口打开和 VAE 或 AE 之间的更多联系，请查看这些很棒的文章在新窗口打开。

引用

@article{karagiannakos2022diffusionmodels,
    title   = "Diffusion models: toward state-of-the-art image generation",
    author  = "Karagiannakos, Sergios, Adaloglou, Nikolaos",
    journal = "https://theaisummer.com/",
    year    = "2022",
    howpublished = {https://theaisummer.com/diffusion-models/},
  }

参考文献

许可协议

注意

本站所有内容均使用 MIT 协议，请遵守此协议。转载请标明出处：shao.fun在新窗口打开

# 扩散模型是如何工作的：从零开始的数学原理

# 译者前言

# 扩散模型是什么？

# 扩散过程

# 前向扩散

# 重参数化技巧：在任何时间步长上的可操作闭式采样

# 方差表

# 反向扩散

# 用神经网络逼近反向过程

# 训练一个扩散模型

# 架构

# 条件性图像生成：引导扩散

# 分类指导

# 无分类指导

# 扩大扩散模型的规模

# 级联扩散模型

# Stable Diffusion: 潜在扩散模型

# 基于评分的生成模型

# 为基于评分的模型添加噪音：噪声条件得分网络 (NCSN)

# 通过随机微分方程 (SDE) 进行基于评分的生成性建模

# 总结

# 引用

# 参考文献

# 许可协议